Невидимый эксперт. Часть 1: Как AI влияет на профессиональную самооценку пользователей

Введение

Одним из самых полезных инструментов в любой сфере деятельности на текущий момент считается искусственный интеллект. Его польза очевидна по многим исследованиям (The Quarterly Journal of Economics, ScienceDirect), он помогает увеличить эффективность, снижает нагрузку рутинными задачами и экономит время на поиск.

В противопоставление очевидным плюсам хотелось бы выделить и менее очевидный эффект: подсознательно люди реже воспринимают результат как собственное достижение. Работа выполняется быстрее, а вместе с тем растет и объем задач, но чувство профессиональной уверенности ослабевает. Выгорание снижается, удовлетворенность профессией падает? В этом исследовании мы попытались разобраться, как использование генеративных моделей влияет на внутреннее ощущение себя как специалиста: профессиональную самооценку, доверие к собственному мышлению и психологический комфорт. Мы сравнили пользователей AI и тех, кто отказывается от его использования, дополнив количественные данные интервью с экспертами рынка труда и специалистами в области психического здоровья.

Результаты, полученные нами в ходе исследования, показали: искусственный интеллект способен снизить уровень выгорания, но одновременно может негативно влиять и на ощущение собственной профессиональной ценности. Этот парадокс стал центральной темой исследования.

Статистическое исследование

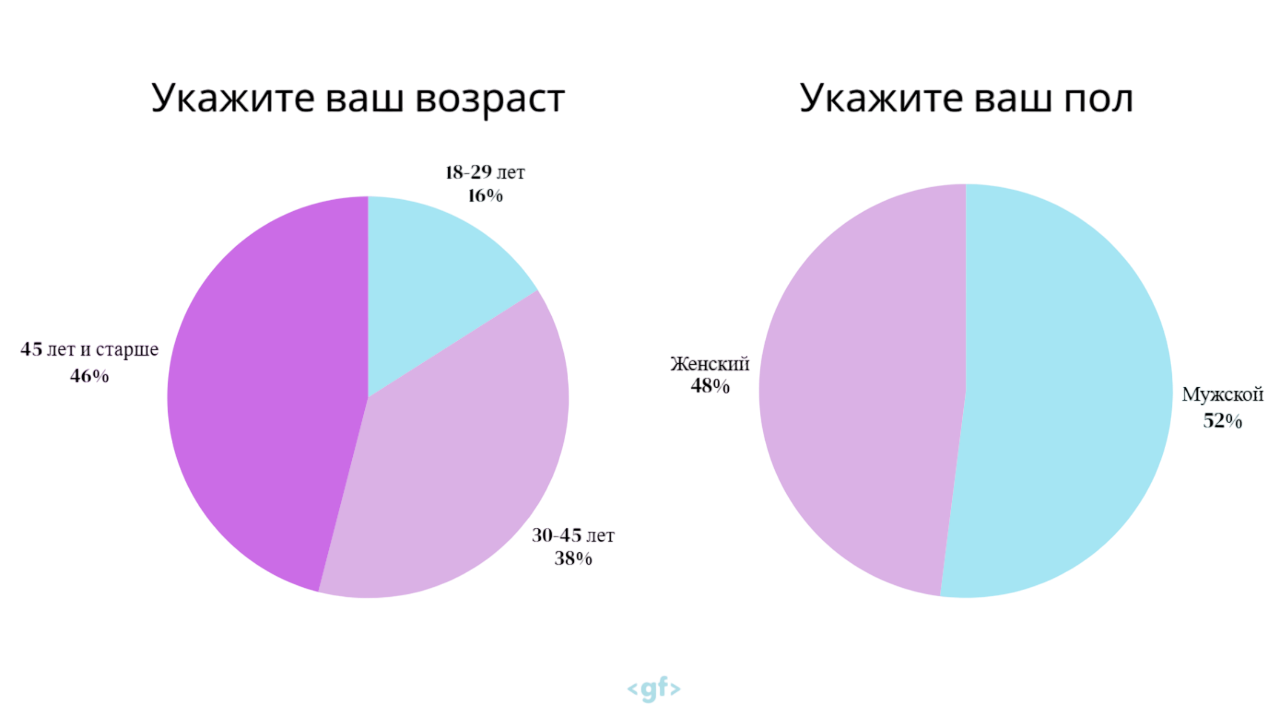
В рамках нашего исследования был проведён опрос среди трудоспособного населения. Целью опроса стало определить распространенность использования генеративных моделей и сравнить уровни выгорания и уровни удовлетворенности профессиональным путем среди населения, использующего AI-инструменты, и населением, которое их не использует. В опросе приняли участие 125 респондентов. Возрастное распределение: 46% участников старше 45 лет, 38% находятся в диапазоне 30–45 лет, 16% молодые специалисты 18–29 лет. Гендерное распределение близко к симметричному (52% мужчины, 48% женщины), исходя из чего мы можем считать минимальными возможные смещения, связанные с половыми различиями.

Диаграмма 1,2. Возраст и пол респондентов.

Профессиональный стаж респондентов: 48% работают в своей сфере семь лет и более, еще 19% от четырех до шести лет. Специалисты с опытом один-три года составили 24%, начинающие 9%. Отраслевое распределение респондентов также оказалось разнообразным. Наиболее частыми сферами респондентов стали IT (31%), инженерия и строительство (15%), HR (11%), государственное управление, право и безопасность (10%), а также направления, связанные с культурой, медиа и творческими индустриями (10%). Остальные профессии объединены в категорию «другое» (17%).

Диаграмма 3,4. Профессиональная сфера и профессиональный стаж.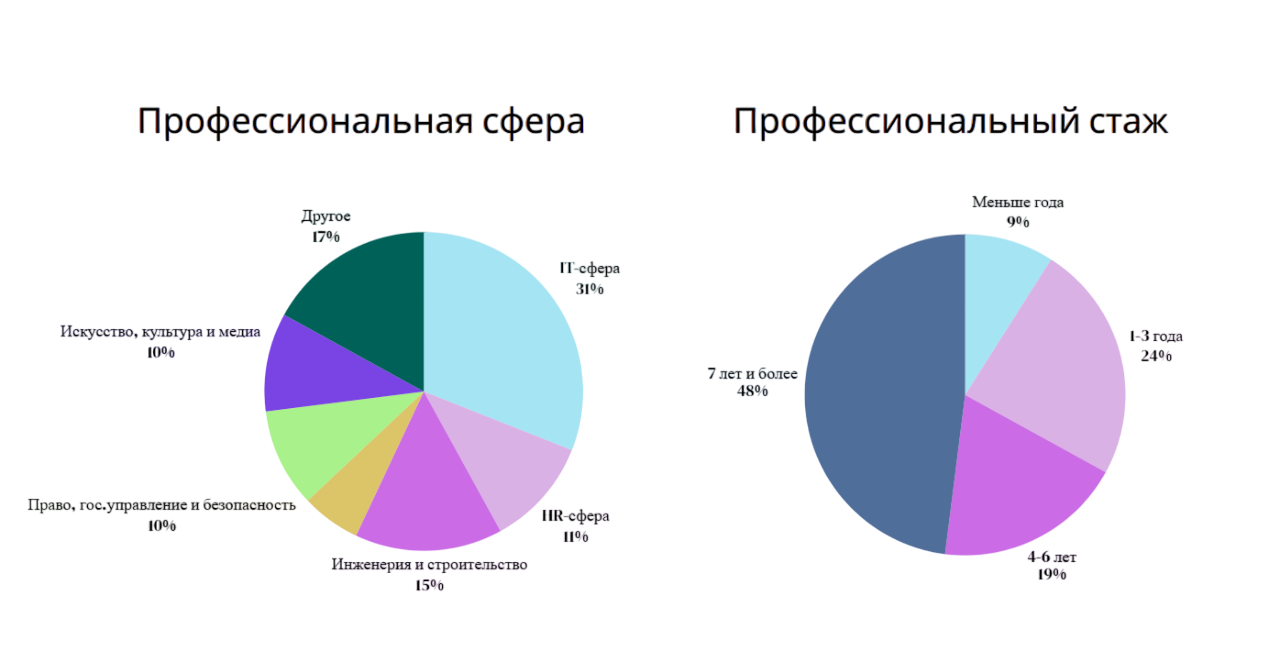

80% респондентов отметили, что используют AI. Среди них практически одинаковое соотношение по применению в повседневных делах и профессиональной деятельности.

Диаграмма 7,8,9. Статистика использования AI

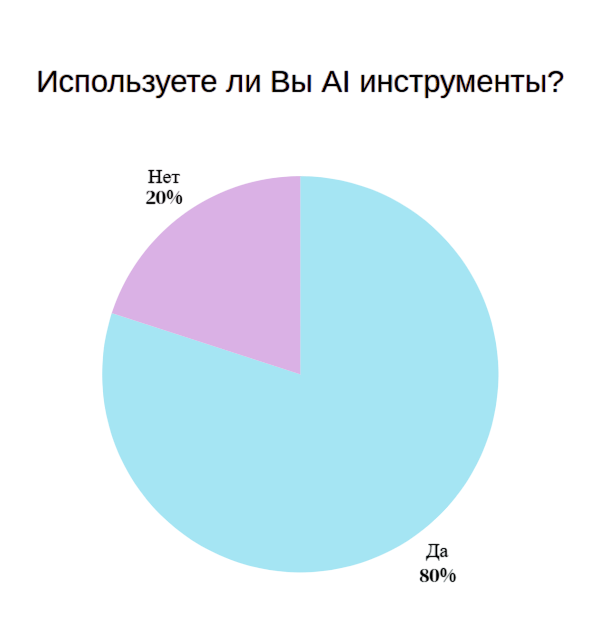
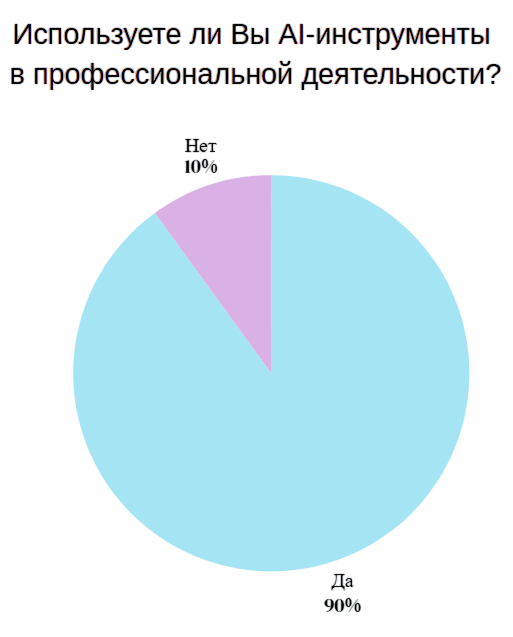
Половина использующих генеративные модели респондентов взаимодействует с инструментами ежедневно: 54% ограничиваются десятью запросами в день, 21% превышает этот показатель.

Диаграмма 10. Частота использования AI

Наибольший уровень доверия респонденты продемонстрировали в задачах, связанных с креативом и проверкой фактов. Такие направления, как финансы и медицина, воспринимаются заметно осторожнее. Около трети пользователей отметили, что не готовы доверить в приоритете генеративным моделям ни одну из категорий задач.

Диаграмма 11. Сферы доверия к AI

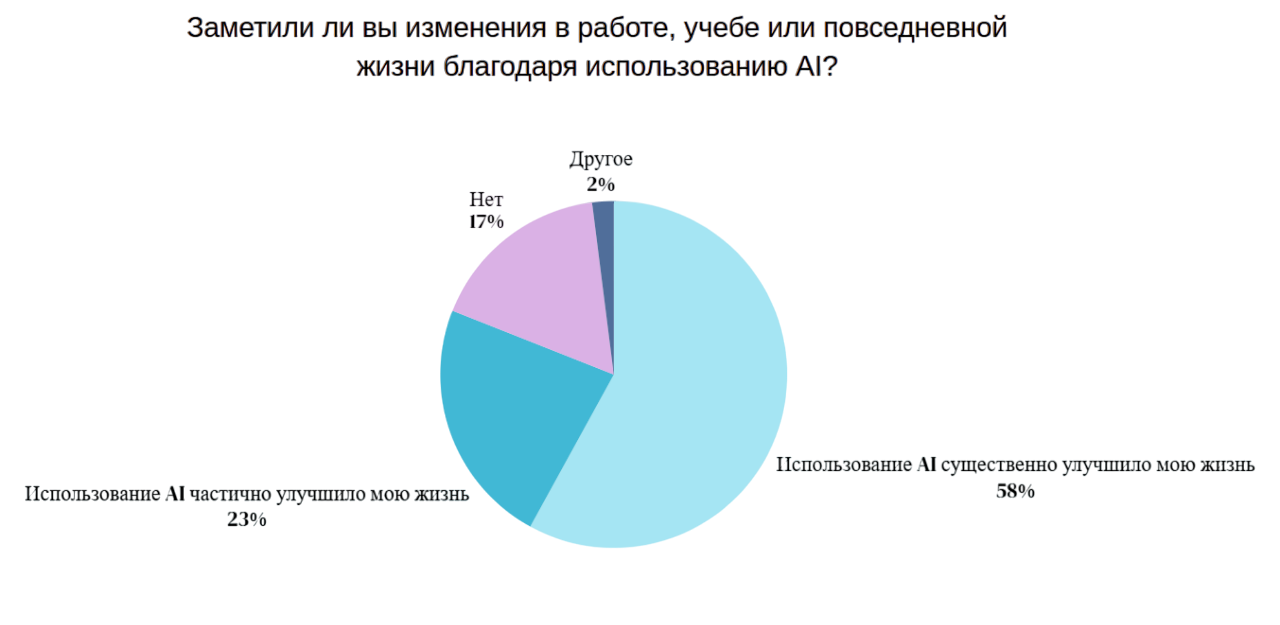
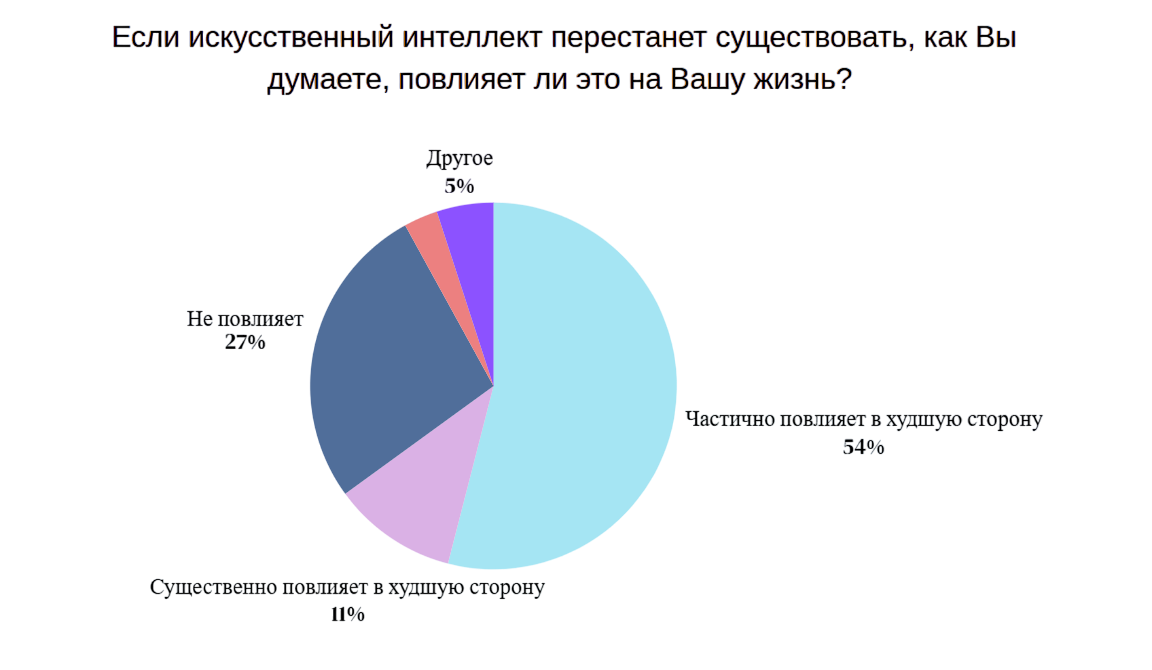
Субъективная оценка изменения жизни из-за влияния AI: 58% отметили существенное улучшение уровня жизни, 23% частичное, 17% не зафиксировали заметных изменений. В сценарии гипотетического исчезновения AI 54% респондента ожидают ухудшения качества жизни, 27% не видят существенных последствий, 5% затруднились с ответом.

Диаграмма 12,13. Субъективная оценка влияния AI на жизнь

Средний показатель уровня выгорания у респондентов, использующих AI, составил 4,87 (по шкале от 1 до 10, где 10 - максимальный уровень выгорания). Также средний показатель уровня удовлетворения профессиональным путем у респондентов, использующих AI, составил 6,08 (по шкале от 1 до 10, где 10 - максимальный уровень удовлетворения своим профессиональным путем)

Диаграмма 14,15. Уровень выгорания и удовлетворенности проф.путем респондентов, использующих AI

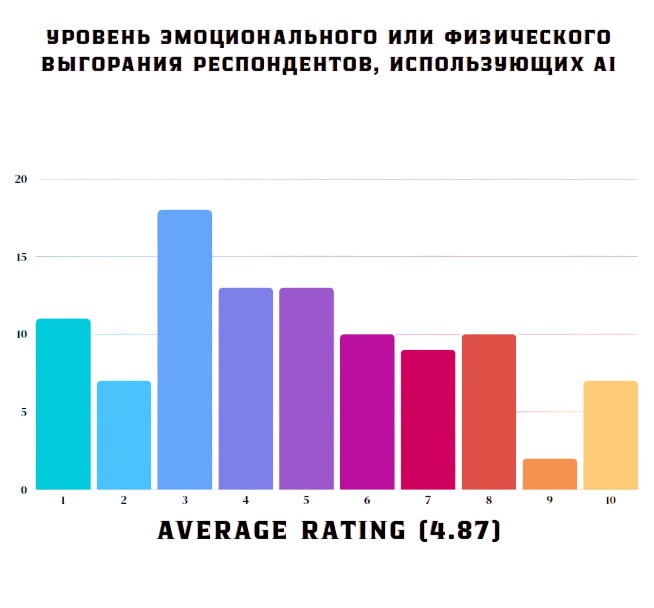
Если говорить о респондентах, не использующих AI, то около 40% участников этой подвыборки считают причиной для отказа от генеративных моделей недостаточное доверие к точности их работы. Примерно столько же из подвыборки считают, что подобные технологии им не нужны.

Диаграмма 16. Причины отказа респондентов от использования AI

При этом лишь 4% вообще не знакомы с технологиями AI, а 64% респондентов всё же имеют поверхностное представление (“слышал, но не применяю”), и 32% хорошо осведомлены о функциях и возможностях AI , но целенаправленно по своему решению избегают его использования.

Диаграмма 17. Осведомленность респондентов о AI-инструментах

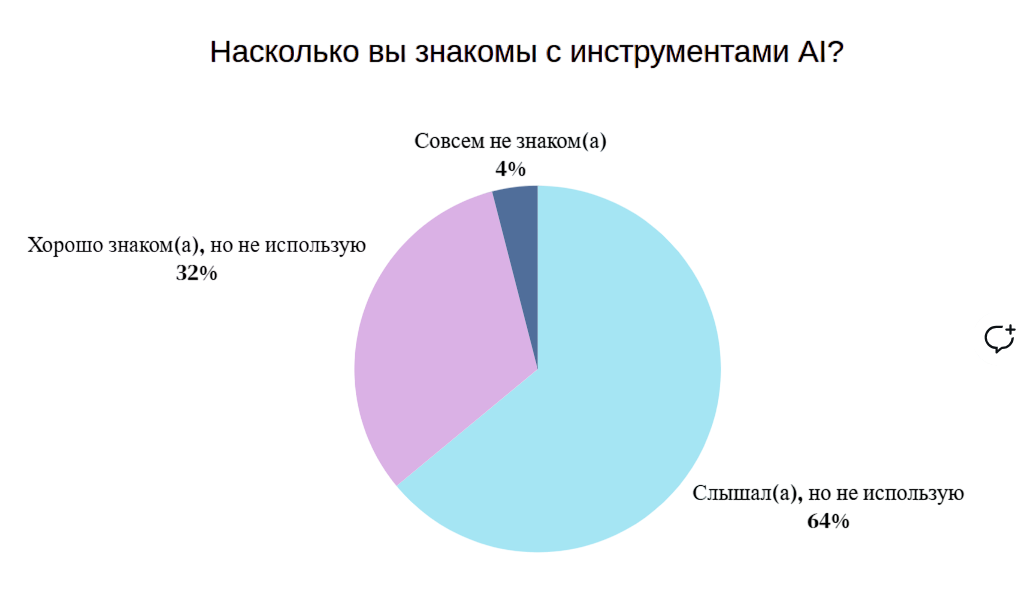
Некоторые респонденты, не использующие генеративные модели, также отметили, что согласились бы изучить основы их применения в рамках обучения.

Диаграмма 18. Основные факторы мотивации к использованию AI

Прим.автора: Дополнительной диаграммой стоит вынести возрастное распределение выборки, не использующей AI-инструменты.

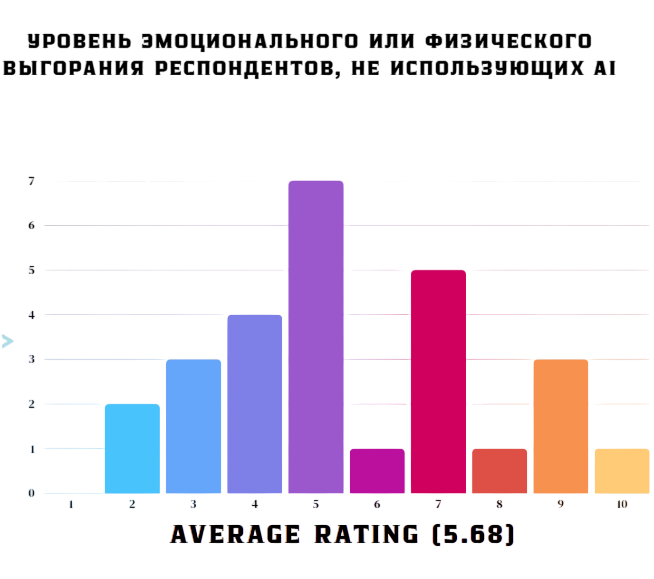
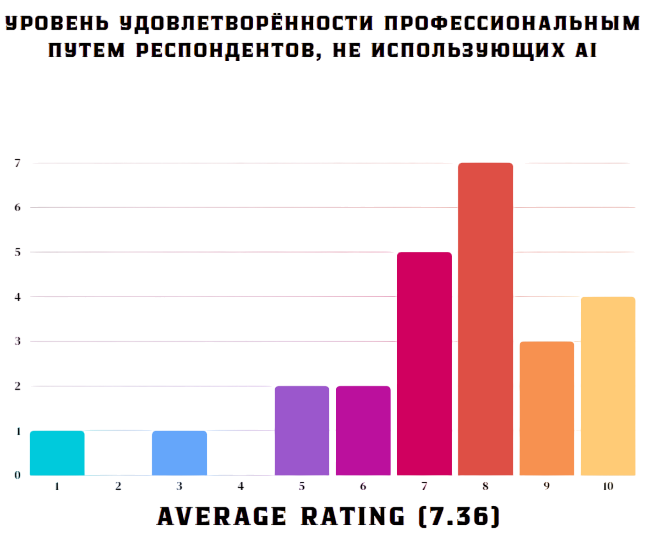
Средний показатель уровня выгорания у респондентов, не использующих AI, составил 5,68 (по шкале от 1 до 10, где 10 - максимальный уровень выгорания). Средний показатель уровня удовлетворения профессиональным путем у респондентов, не использующих AI, составил 7,36 (по шкале от 1 до 10, где 10 - максимальный уровень удовлетворения своим профессиональным путем).

2. Расчеты.

Сравнение удовлетворенности карьерой между пользователями ИИ и не пользователями ИИ.

В связи с небольшим объемом выборки для оценки уровня удовлетворенности карьерой респондентов были выделены две группы: пользователи ИИ, использующие генеративные модели в работе, далее - Пользователи ИИ (n = 89) и не пользователи ИИ (n = 25). Каждому участнику был присвоен балл по шкале от 1 до 10.

1. Распределение оценок и расчет среднего

Таблица 1. Группа пользователей ИИ (n = 89)

Оценка	Количество	Оценка × Количество
10	5	50
9	7	63
8	18	144
7	16	112
6	10	60
5	11	55
4	7	28
3	6	18
2	5	10
1	4	4
Итого	89	544

Среднее: $$= $\frac{544}{89}$ = 6,11

Стандартное отклонение = $s_{1}$ = √(Σ($x_{i}$ - x̄)² / (n-1)) = 2,39

Находим $x_{i} -$ для каждой оценки (вспом.табл 1)

x_i	x_i - 6,11	x_i	x_i - 6,11
10	3,89	5	-1,11
9	2,89	4	-2,11
8	1,89	3	-3,11
7	0,89	2	-4,11
6	-0,11	1	-5,11

Возводим каждое отклонение в квадрат (вспом.табл 2):

x_i	(x_i - 6,11)² * Количество ответивших	x_i	(x_i - 6,11)² * Количество ответивших
10	15,13 * 6 ≈ 75,66	5	1,23 * 11 ≈ 13,55
9	8,35 * 7 ≈ 58,47	4	4,45 * 7 ≈ 31,16
8	3,57 * 18 ≈ 64,30	3	9,67 * 6 ≈ 58,03
7	0,79 * 18 ≈ 12,67	2	16,89 * 5 ≈ 84,46
6	0,0121 * 10 ≈ 0,121	1	26,11 * 4 ≈ 104,45

Находим s: Сумма всех квадратов разностей$\Sigma(x_{i}\ - \ 6,11)²\ *\ Количество\ ответивших$ = 502,87
Дисперсия выборки = n - 1 = 89 - 1 = 88, дисперсия = $\frac{502,87}{88}$ = 5,71
Стандартное отклонение $s_{1}$ =√5,71 $$ = 2,39

Таблица 2. Группа не пользователей ИИ (n = 25)

Оценка	Количество	Оценка × Количество
1	1	1
3	1	3
5	2	10
6	2	12
7	5	35
8	7	56
9	3	27
10	4	40
Итого	25	184

Прим.автора: далее расчёты будут указаны без демонстрации основных формул.

Среднее: $$= $\frac{184}{25}$ = 7,36

Стандартное отклонение = $s_{2}$ = √(Σ(x_i - x̄)² / (n-1)) = 2,06

4.Welch t-test

Формула для t-статистики:

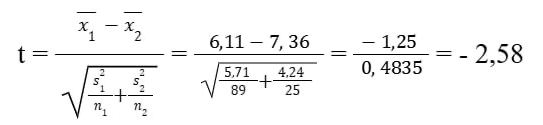
Степени свободы (Welch-Satterthwaite):
df = $\frac{\left( \frac{s_{1}^{2}\ }{n_{1}} + \frac{s_{2}^{2}\ }{n_{2}} \right)^{2}}{\frac{\left( \frac{s_{1}^{2}\ }{n_{1}} \right)^{2}}{n_{1} - 1} + \frac{\left( \frac{s_{2}^{2}\ }{n_{2}} \right)^{2}}{n_{2} - 1}}$ = $\left( \frac{5,71\ }{89} + \frac{4,24\ }{25} \right)^{2} \div \left( \ \frac{\left( \frac{5,71\ }{89} \right)^{2}}{88} + \frac{\left( \frac{4,24\ }{25} \right)^{2}}{24} \right)$ ≈ 43,9

Определяем p-value через таблицу распределения Стьюдента (t-распределение):

1. Рассчитанное t: - 2,58. Степени свободы: df ≈ 43,9.

2. Из в таблицы t-распределения узнаем, какая вероятность (двусторонняя) соответствует |t| (т.к. распределение Стьюдента симметрично относительно нуля) = 2,58 при df ≈ 43,9.

3. Двустороннее p-value из таблицы попадает между 0,025 и 0,01:
   Применив формулу линейной интерполяции, можем найти нужно найти приблизительное значение p-value,
   $y\ = \ y_{0} + \ \frac{\left( x\ - \ x_{0} \right)}{\left( x_{1} - x_{0} \right)} \times \left( y_{1} - y_{0} \right),$ где $x_{0},\ x_{1}$​ - точки, между которыми интерполируем;
   $y_{0\ },\ y_{1}$​ - значения функции в этих точках;
   $x_{}$ - точка, для которой ищем $y_{}$- интерполированное значение.
   Применяем к t-распределению:
   Нижнее и верхнее критическое значение:

$t_{0} = \ 2,414,\ t_{1} = \ 2,692$​
$p_{0} = \ 0,025,\ p_{1} = \ 0,01$
при t = 2,58, выполним расчет p:

$p\ = \ 0,025 + \ \frac{(2.58\ - \ 2,414)}{(2,692\ - 2,\ 414)} \times (0,01 - 0,025)\ \approx \ 0,\ 016,$
p-value для t = 2,58 и df = 43,9 ≈ 0,016.

Рассчитанный p-value означает, что вероятность случайно получить такую разницу между группами всего 1,6%, если нулевая гипотеза верна. Это меньше стандартного уровня значимости 0,05 (5%), который обычно используют в социальных науках.

Исходя из расчетов, разница в уровне удовлетворенности карьерой между пользователями ИИ и не пользователями ИИ является статистически значимой (p < 0,05). В среднем не пользователи ИИ демонстрируют более высокую удовлетворенность карьерой.
Прим. автора: дальнейшие расчеты будут указаны без подробных вспомогательных таблиц для простоты восприятия.

Сравнение уровня выгорания между пользователями ИИ и не пользователями ИИ.
Таблица 3. Группа пользователей ИИ (n = 89)

Оценка	Кол-во участников	Оценка	Кол-во участников
1	10	6	10
2	6	7	8
3	14	8	10
4	12	9	2
5	12	10	5

Среднее: $$= $\frac{487}{89}$ = 4,90
Стандартное отклонение = $s_{1}$ = √(Σ($x_{i}$ - x̄)² / (n-1)) = 2,53

Таблица 4. Группа не пользователей ИИ.

Оценка	Кол-во участников	Оценка	Кол-во участников
2	2	7	5
3	3	8	1
4	1	9	3
5	7	10	1
6	1	1	0

Среднее: $$= $\frac{575}{100}$ = 5,75,
Стандартное отклонение = $s_{2}$ = √(Σ(x_i - x̄)² / (n-1)) = 2,24, s1 = 2,53

4.Welch t-test

Формула для t-статистики: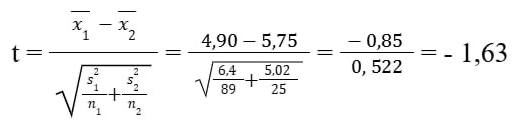

Степени свободы (Welch-Satterthwaite):
df = $\frac{\left( \frac{s_{1}^{2}\ }{n_{1}} + \frac{s_{2}^{2}\ }{n_{2}} \right)^{2}}{\frac{\left( \frac{s_{1}^{2}\ }{n_{1}} \right)^{2}}{n_{1} - 1} + \frac{\left( \frac{s_{2}^{2}\ }{n_{2}} \right)^{2}}{n_{2} - 1}}$ = $\left( \frac{6,4\ }{89} + \frac{5,02\ }{25} \right)^{2} \div \left( \frac{\left( \frac{6,4\ }{89} \right)^{2}}{88} + \frac{\left( \frac{5,02\ }{25} \right)^{2}}{24} \right)$ ≈ 42,76

Определяем p-value через таблицу распределения Стьюдента (t-распределение):

4. Рассчитанное t: - 1,63. Степени свободы: df ≈ 42,76.
   Из в таблицы t-распределения узнаем, какая вероятность (двусторонняя) соответствует |t| = -1,63 при df ≈ 42,76.

5. Двустороннее p-value из таблицы попадает между 0.010 и 0.012:
   Применив формулу линейной интерполяции, можем найти нужно найти приблизительное значение p-value,
   $y\ = \ y_{0} + \ \frac{\left( x\ - \ x_{0} \right)}{\left( x_{1} - x_{0} \right)} \times \left( y_{1} - y_{0} \right),$ где $x_{0},\ x_{1}$​ - точки, между которыми интерполируем;
   $y_{0\ },\ y_{1}$​ - значения функции в этих точках;
   $x_{}$ - точка, для которой ищем $y_{}$- интерполированное значение.
   Применяем к t-распределению:
   Нижнее и верхнее критическое значение:

$t_{0} = \ 2,64,\ t_{1} = \ 2,704$​
$p_{0} = \ 0,012,\ p_{1} = \ 0,010$
при t = 1,63, выполним расчет p:

$p\ = \ 0,012 + \ \frac{(1,63\ - \ 2,64)}{(2,704\ - 2,\ 64)} \times (0,010 - 0,012)\ \approx \ 0,\ 0196\ \approx \ 0,02$
p-value для t = 2,58 и df = 43,9 ≈ 0,02.

Рассчитанный p-value означает, что вероятность случайно получить такую разницу между группами всего 2%, если нулевая гипотеза верна. Это меньше стандартного уровня значимости 0,05 (5%), который используют в социальных науках.

Исходя из расчетов, разница в уровне выгорания между пользователями ИИ и не пользователями ИИ является статистически значимой (p < 0,05). В среднем группа “не пользователи ИИ” демонстрируют более высокий уровень выгорания по сравнению с “пользователями ИИ”.

По результатам статистического исследования можно заключить, что использование генеративных моделей негативно сказывается на ощущении профессиональной компетенции, но при этом также оказывает положительное влияние на уровень выгорания.

Продолжение исследования

В следующей части читайте о возможности возникновения нехимической зависимости от AI, дополненное мнением практикующего психиатра: Невидимый эксперт, Часть 2: Возникновение нехимической зависимости от AI

Дорогие коллеги!

Команда Geekfactor искренне благодарит вас за внимание к данной теме. Мы будем рады ознакомиться с вашими мыслями и комментариями, для оперативной связи просто напишите Екатерине.

Если у вас есть тема которую вы бы хотели обсудить, подпишитесь на наш канал - будем рады вашим комментариям. Мы рады любым возможностям совместного сотрудничества!